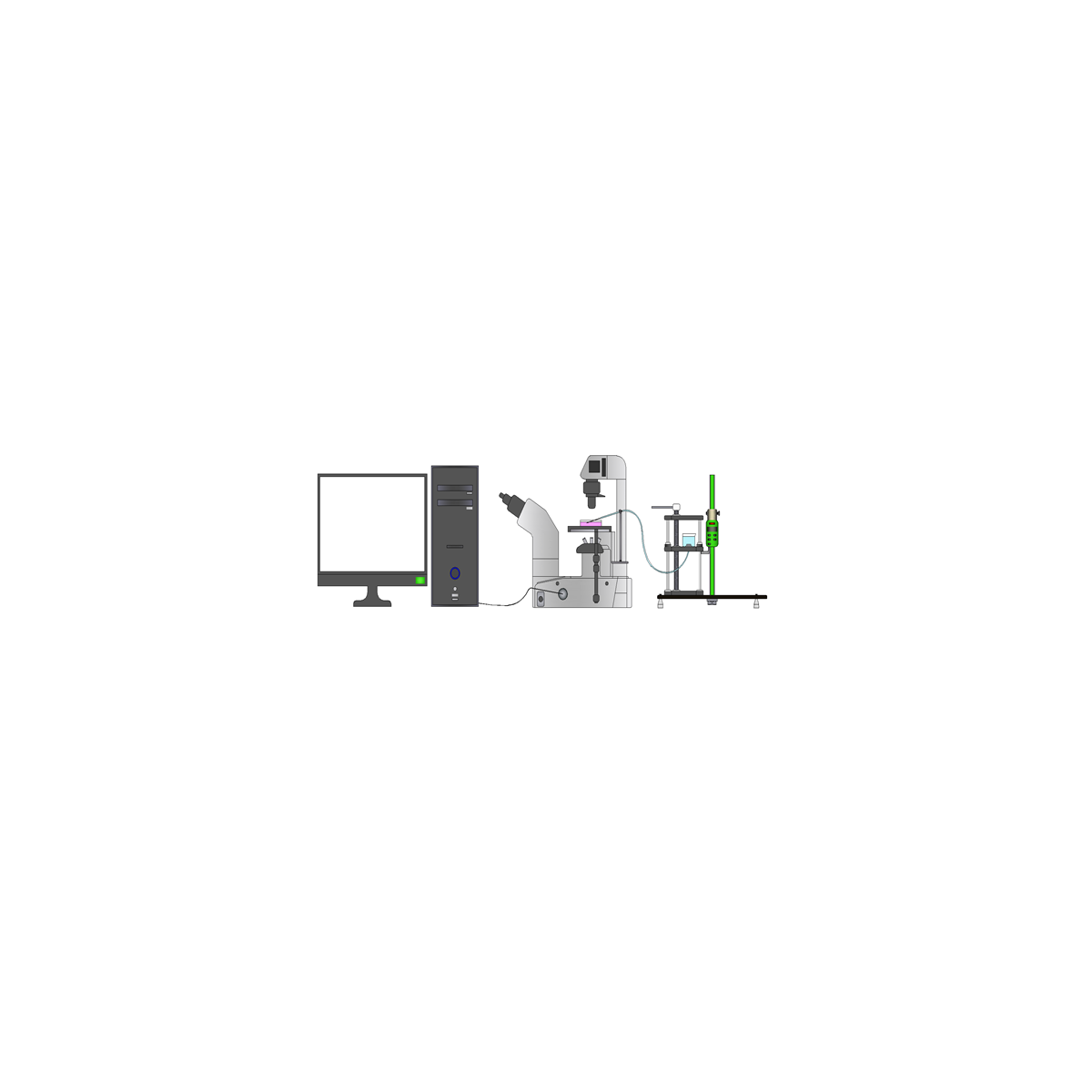
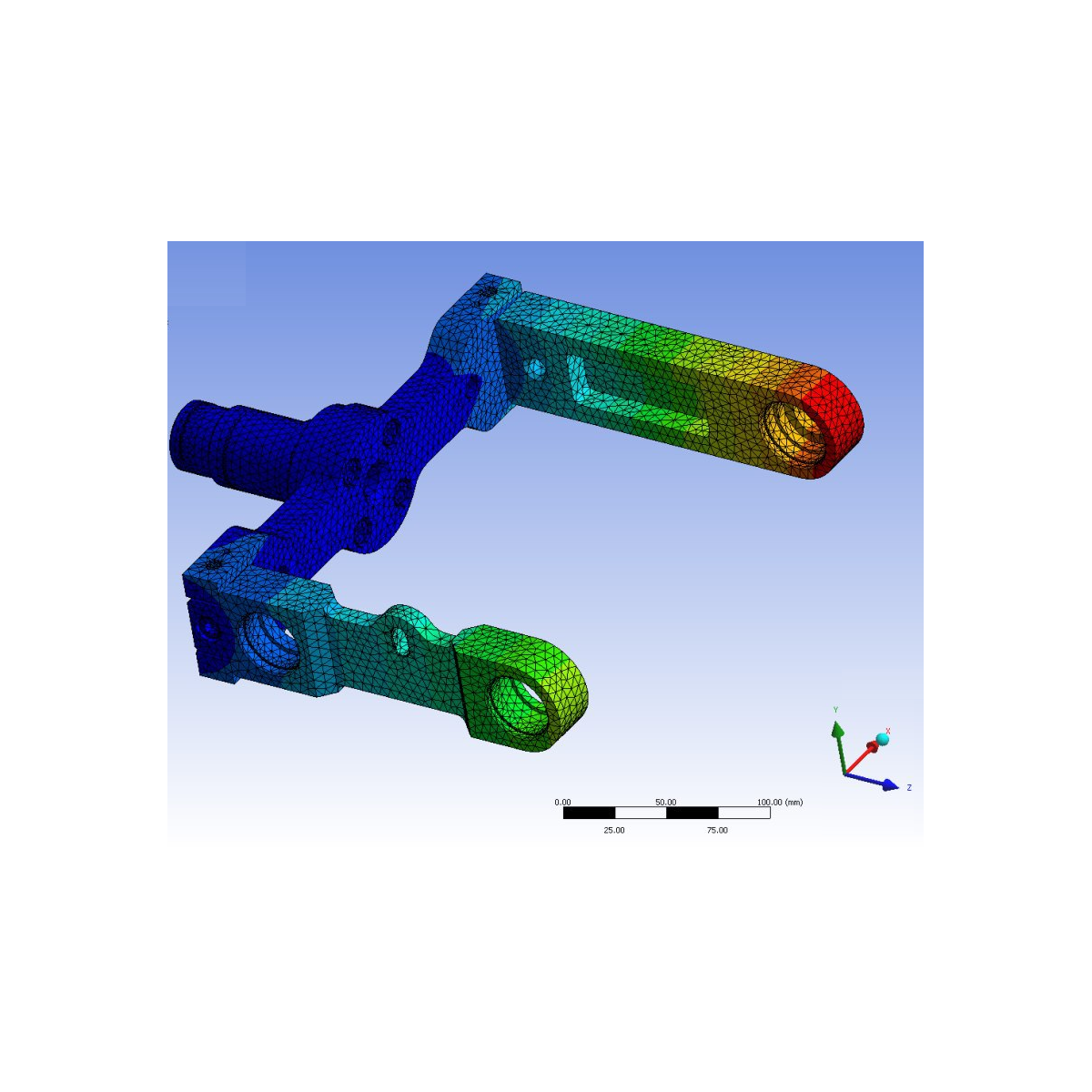
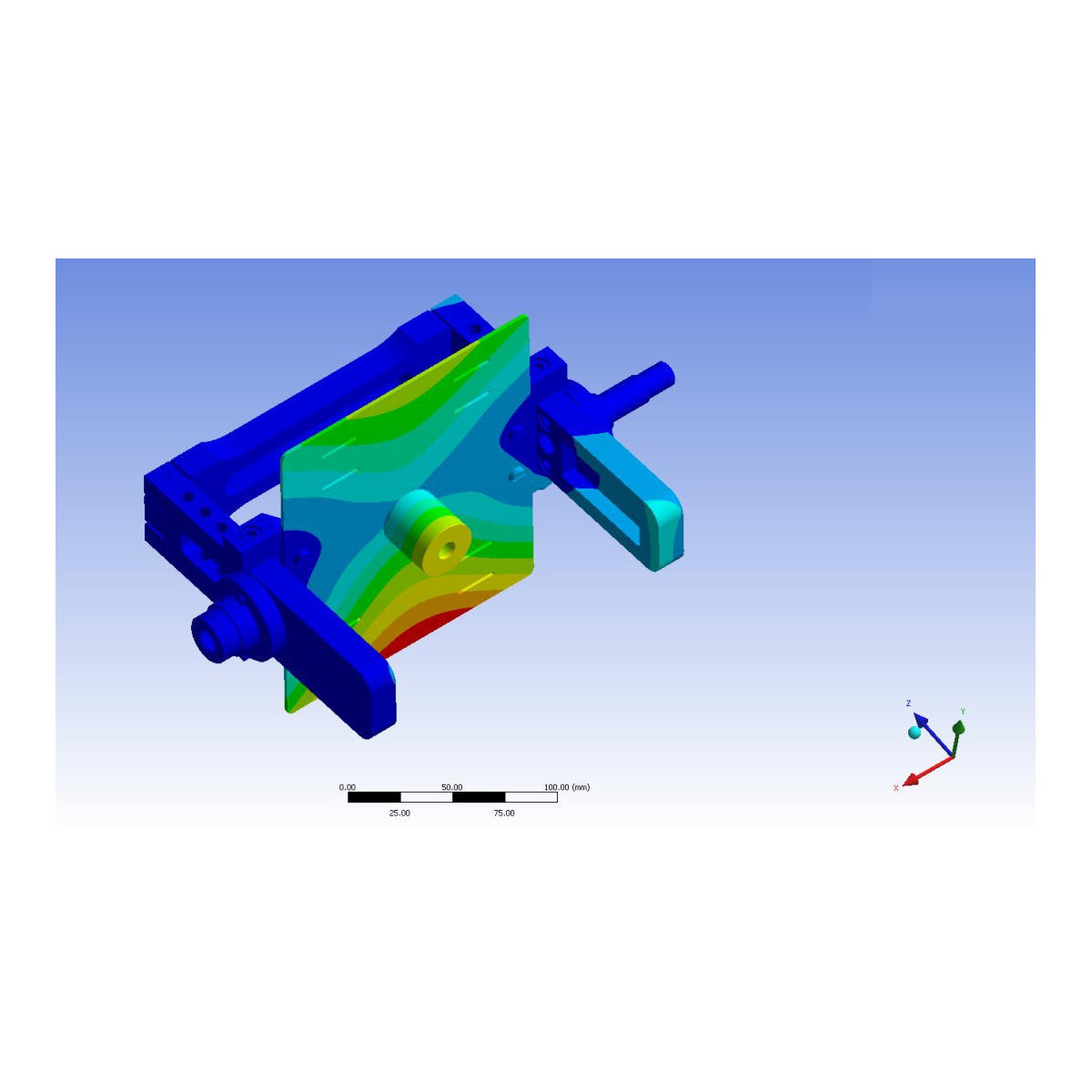
Biological tissues are roughly divided into hard tissues like bone and tooth and soft tissues such as cartilage, liver, blood vessel. The mechanical properties of soft and hard tissues are different because of the mineral content. One of the significant differences is that soft tissues are more deformable than hard tissues. Therefore, applied infinitesimal deformation for industrial materials such as metals cannot be used for soft tissues. Instead, finite deformation theories are often used to describe the mechanical behavior of soft tissues. From this point of view, the experimental integrated simulations of the soft tissues are required.
Current Projects
MRI-based simulation of knee articular cartilage
Finite element modelling can be used to evaluate altered loading conditions and failure locations in knee joint tissues. Besides material properties and experimental comparison, the main limitation of this modelling approach has been exact geometry. MRI techniques not only can provide the exact geometry, but also its results can be used to determine the diffusion tensor of cartilage. Our study aims to provide biphasic constitutive model to based on the MRI data to have sample/patient-specific models.
Previous Projects
Impact of simulated microgravity on viscoelastic properties of cells
Microgravity condition leads to endothelium dysfunction which in turn causes the individuals to experience cardiovascular deconditioning as well as physiologic changes. Gravitational alterations influence endothelial cell (EC) proliferation, differentiation, signaling, gene expression, surface adhesion molecules, extracellular matrix proteins expression, and cause significant changes in cytoskeletal polymers. The goal of this study was to investigate the impact of s-μg on viscoelastic parameters of ECs and the content of main cytoskeleton polymers. A developed RPM was utilized to simulate weightless conditions by means of continuous random change of orientation, relative to the gravity vector.

Michael Mellinger
Dipl.-Ing. (FH)Technical Staff

Seyed Morteza Seyedpour
Dr.-Ing.Head of Laboratories, Head of Experimental Mechanics & Enviromental Engineering Group, Researcher