Brain Tumour Modelling

The medical relevance of brain tumours is mainly reflected by a high mortality rate (83 of 100 incidences, 2016, Germany) and a low remaining life expectancy (approx. 4 years from onset of disease to death, 2016, Germany). Within that interdisciplinary topic, a data-integrated continuum-mechanical modelling approach is investigated to bring insights into the relevant processes of tumour growth and regression in brain tissue.

How can data-integrated models help to better understand the growth and regression processes of brain tumours and increase the therapeutic success of medical treatments?

In order to perform patient-specific simulations to predict, for example, the actual spread of mobile cancer cells, or the severity of tumour disease in the brain, we propose a data-based continuum-mechanical modelling approach, which is shown schematically in Figure 1.

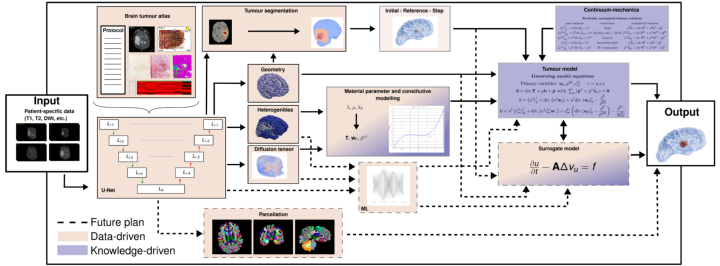
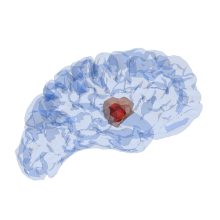
According to this, the patient data already collected from a medical diagnosis are used as input parameters. Primarily, these consist of magnetic resonance imaging (MRI) scans of various modalities, but can also contain more general information such as age, sex or weight. This information is then processed in a convolutional neural network shaped as an U-Net with skip connections. The U-Net is trained to medical data from various studies, such as IvyGAP [3] or TCIA (www.cancerimagingarchive.net) of healthy and diseased brains in the form of a brain tumour atlas. This contains related MRI scans, recorded disease progression, histological sections (ISH and H&E-stained, segmented tumour feature maps) and segmented gene expressions from tissue samples, as well as already segmented 3-D tumours. The input is filtered and processable information is collected. This then results in: the geometry of the brain, spatially distributed specific properties such as heterogeneities and flow properties and also the most accurate possible position and composition of the tumour is gained through  a segmentation process. With all this information, initial boundary value problems can then be set up in the framework of the Theory of Porous Media, see [4]. In Figure 2, a test calculation of the left hemisphere of a processed brain is shown. The nutrient demand of a tumour correlates with its increasing size, which at a certain point leads to collapse and the inner core of the tumour is undersupplied and dies. The characteristic profile of a tumour (necrotic core and active cell mass inside, mobile cells outside), is thus represented by the model, see [2].

Figure 2: The left hemisphere of a test case from [1] is processed from MRI scans into a finite-element mesh. An initial mobile cancer cell concentration is set at t₀ and spreads during the simulation (t₁) into the surrounding domain. At the final time step t₂ a solid core n^St is formed and the concentration of the mobile cancer cells is widely spread.

In addition to the accuracy of the resulting statements, the required processing time is also significant for clinical use. Therefore, a possible extension is shown by dashed lines in Figure 1. In that, the constitutive laws required for the continuum-mechanical model are replaced by another machine learning approach in order to represent the comprehensive reality. Furthermore, critical locations have to be identified from the U-Net via a parcellation in order to be able to determine the severity of the tumour more precisely. Finally, the idea is to speed up the workflow by replacing the comparatively expensive model with a simpler surrogate model.

[1] K.-A. Mardal et al.
Mathematical modeling of the human brain.
Springer Nature, 2021.

[2] M. Suditsch et al.
Application of a continuum-mechanical tumour model to brain tissue.
PAMM, 21(1), 2021.

[3] R. B. Puchalski et al.
An anatomic transcriptional atlas of human glioblastoma.
PMC, 360:660–663, 2019.

[4] A. Wagner.
Continuum Mechanics of Multicomponent Materials.
Habilitation thesis, University of Stuttgart, 2021.