Basics
Articular cartilage, like shown in Fig. 1, is part of the connective tissue of humans and animals. As the only type of connective tissue does it not dispose on an important part of cells. It’s a multi-phase material consisting of fluids, electrolytes and solid parts. The parts can be split in proteoglycans und collagen fibers. The proteoglycans compose the extracellular matrix (ECM), which generates the shape of the tissue und with it the shape of the articular cartilage. The Function of the ECM is the fixation of the collagen fibers in the tissue. In articular cartilage are most of the collagen fibers from type II (~95%). The ECM is streamed by the second phase, the fluid. The fluid consists of tissue water resinated with electrolytes. The volume fraction of the fluid phase, depending on the creature, is in between 30% to 50% of the mass fraction. This is much more as all other connective tissue. The collagen fibers also include fluid. This fluid is fixed in the fibers and cannot squeezed out without damage the fiber, this fluid has only an indirect influence on the stiffness of the collagen fibers. This observation led to the mechanical properties of the articular cartilage. It is a porous material with incompressible, transverse-isotropic material behavior for the fluid as well as the solid. This means the distribution and orientation of the fibers is the central point for the permeability as well as the deformation of the solid fraction.
In our model we consider different effects to describe articular cartilage in a physical and chemical realistic way, like biphasic material behavior, transverse isotropy, osmosis and damage and ageing.
Patient specific treatment
With our cooperation partners David Pierce and Gerhard Holzapfel we develop a patient specific continuum model of articular cartilage, to get individual solutions for single patients. To understand the behavior of cartilage better, it is necessary to get individual information of the articular cartilage. An Example is shown in Fig. 2.
The Figure shows a MPM (multi-photon-microscope) image, this technique works with the measure of the velocity of water molecules. With this method it is possible to get undisturbed pictures of living tissue up to a depth of 1 mm. In addition software is included which investigates the collagen fiber dispersion, shown with red beams. The picture shows a knee articular cartilage, it is possible to identify the three typically zones of articular cartilage: depth zone, middle zone and superficial zone.
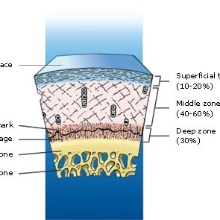
These three zones are shown in Fig.3. In the superficial zone the fibers are parallel to the surface, in the middle zone they change there orientation to normal to the surface and the deep zone with very less fibers. Like shown in Fig.2 the superficial and middle zone are highly anisotropic.
Theory of porous media
To describe this material behavior the theory of porous media (TPM) is used. It is a mixture theory restricted by the concept of volume fraction. The single phases are homogenized to a mixed model. This leads to a smeared model which means at each time t each material point contains both phases. This is shown in Fig.4, the kinematics. Two independent motion functions are needed, one for each phase.
The concept of volume fraction and the volume and saturation conditions are used to describe the behavior of the single phases in a physical realistic way.
Transverse Isotropy
The stiffness and the stability of the articular cartilage depends pridominat on the permeability and the fiber dispersion. To take this into account the fiber dispersion is considered in the model which leads to isotropic and transverse isotropic stress parts as well as isotropic and transverse depending parts for the permeability.
Osmosis
Like discussed before, articular cartilage contains electrolytes. This is the reason for local chemical disequilibriums which lead to osmotic pressure in the articular cartilage.
The Fig.5 shows the basic osmosis of fluids with different concentrations. The Fluid with less concentration flows in the higher one to decrease the concentration until there is an equilibrium. The different concentrations in the articular cartilage are caused by ions which are fixed in matrix material and cannot move free in the fluid. Hence, the articular cartilage is pre-stressed.
Damage and ageing
With regard to the patient specific information it is interesting to describe disease pattern in articular cartilage, like arthrosis or osteoporosis. Therefore a damage description is needed. Like the stresses and the permeability it is necessary to take the fiber dispersion into account. Due to the high stiffness of the fibers it is a useful assumption to say that on the one hand damage happens as damage of the fibers which leads to an increase of stiffness (anisotropic damage), and on the other hand the liquidation of the fiber dispersion (isotropic damage). So, the isotropic damage is the damage of the ECM which is responsible for the fiber dispersion.
Literature
- Lilledahl MB, Pierce DM, Ricken T, Holzapfel GA, de Lange Davies C. Structural analysis of articular cartilage using multiphoton microscopy: input for biomechanical modeling. IEEE Trans. Med. Imaging 2011; 30:1635–1648.
- Pierce DM, Ricken T, Holzapfel GA. A hyperelastic biphasic fiber-reinforced model of articular cartilage considering distributed collagen fiber orientations: continuum basis, computational aspects and applications. Comput. Methods Biomech. Biomed. Engin.
- Ricken T, Bluhm J. Evolutional growth and remodeling in multiphase living tissue. Comp. Mater. Sci. 2009; 45:806–811.
- Ricken T, Bluhm J. Remodeling and growth of living tissue: a multiphase theory. Archive Appl. Mech. 2010; 80:453–465.
- Ricken T, Dahmen U, Dirsch O. A biphasic model for sinusoidal liver perfusion remodeling after outflow obstruction. Biomech. Model. Mechanobiol. 2010; 9:435–450.
- Ehlers W. Foundations of multiphasic and porous materials. Porous Media: Theory, Experiments and Numerical Applications, W Ehlers JB (ed.), Springer-Verlag: Berlin, 2002; 3–86.

Franziska Egli
M.Sc.Research Assistant

Tim Ricken
Univ.-Prof. Dr.-Ing.Head of Department