Numerics & Model Order Reduction

Physics-based modeling has been the classical tool for describing and predicting the behavior of multiphysical systems. High fidelity simulations of such systems require suitable numerical schemes as well as fine scale spatio-temporal grids.

Within multiphysics, the proper design of such numerical schemes is challenging. Beside stability, even in the asymptotic ranges of the material parameters, accuracy of primal (e.g., displacement) as well as dual quantities (e.g., stresses) is required. Within many engineering applications accurate dual quantities are even more relevant than the primal ones. Strictly speaking, this requires the incorporation of primal as well as dual quantities into the numerical schemes, enlarging size and complexity of the emerging linear equation systems. In return, this paves the way to construct parameter-robust, adaptive solution strategies, delivering guaranteed accuracy on tailored spatio-temporal grids.

Even with the current advances of computational capabilities, many engineering questions, such as optimization, uncertainty quantification, model-based predictive control or clinical-time constraints require a reduction of computational complexity. Therefore, reconstruction-based techniques, such as equilibration, reduces complexity by calculating sufficiently accurate fluxes based on the primal variables. A direct incorporation into the numerical scheme is therefore not required. A different approach dealing with the same issue is model-order reduction (MOR).

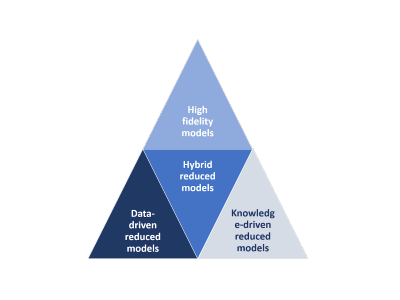
MOR methods have been developed to reduce computational time complex, multiphysical systems while preserving their important physical features. Most popular MOR methods can be classified into three main categories: 1) knowledge-driven approaches utilizing tools such as asymptotic analysis and homogenization. 2) Projection-based methods extracting the essential dynamical features and projecting the models onto those features. 3) Data-driven approaches applying machine learning methods on simulation or experimental data.

In this group we investigate the applicability of different MOR methods and reconstruction-based techniques on different industrial, medical, and environmental applications. Moreover, novel model-reduction methods, based hybrid reduction and reconstruction techniques, will be developed and tested. Our aim is to achieve the most possible fast predictions, while still maintaining acceptable stability and accuracy levels.